In this section, there are 15 questions about Basic Concepts. If you find it difficult to solve the questions; easy-to-understand detailed solutions can be found with the “Click for Solution” option. Good work.


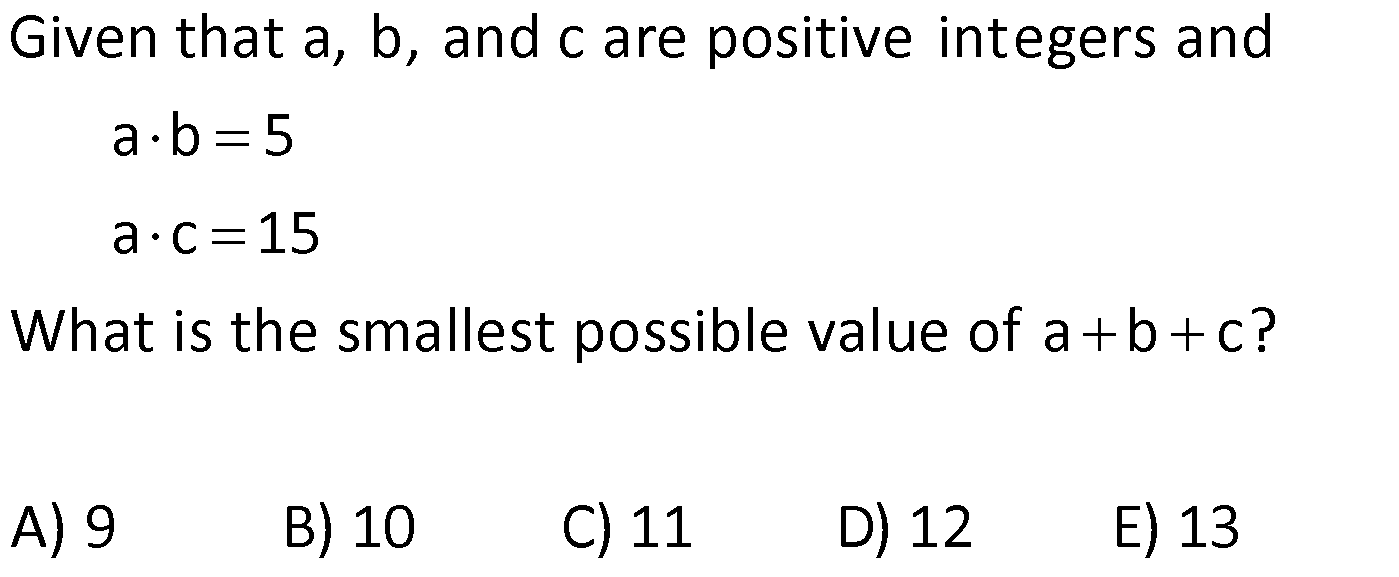



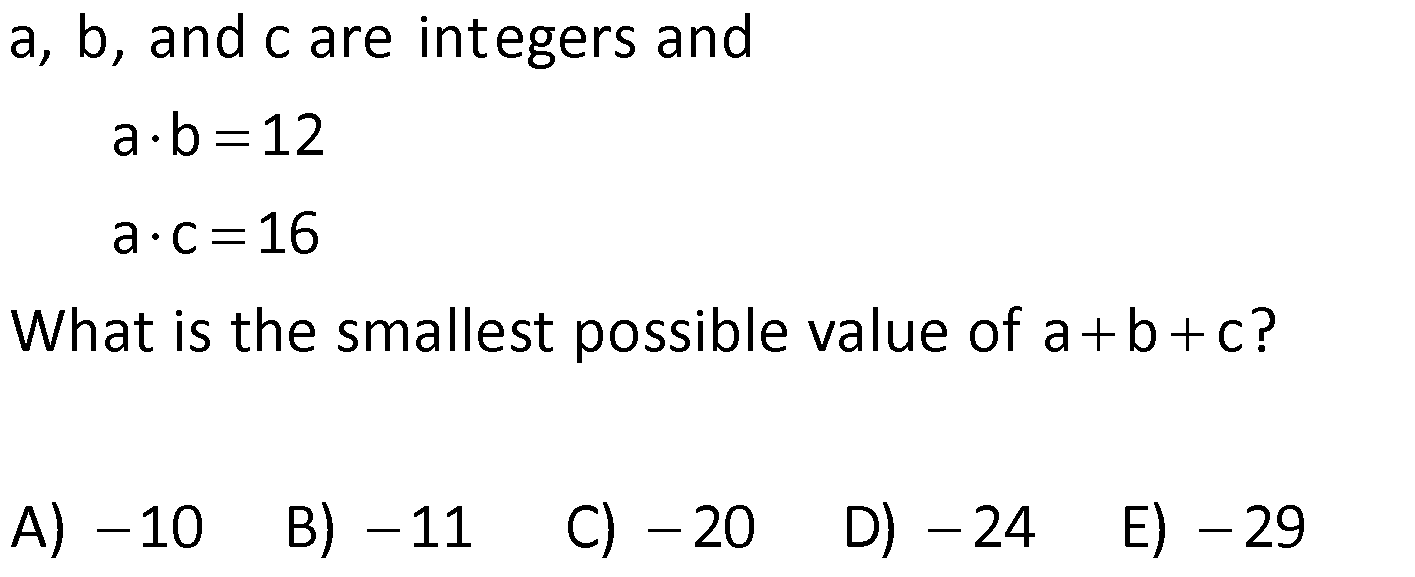



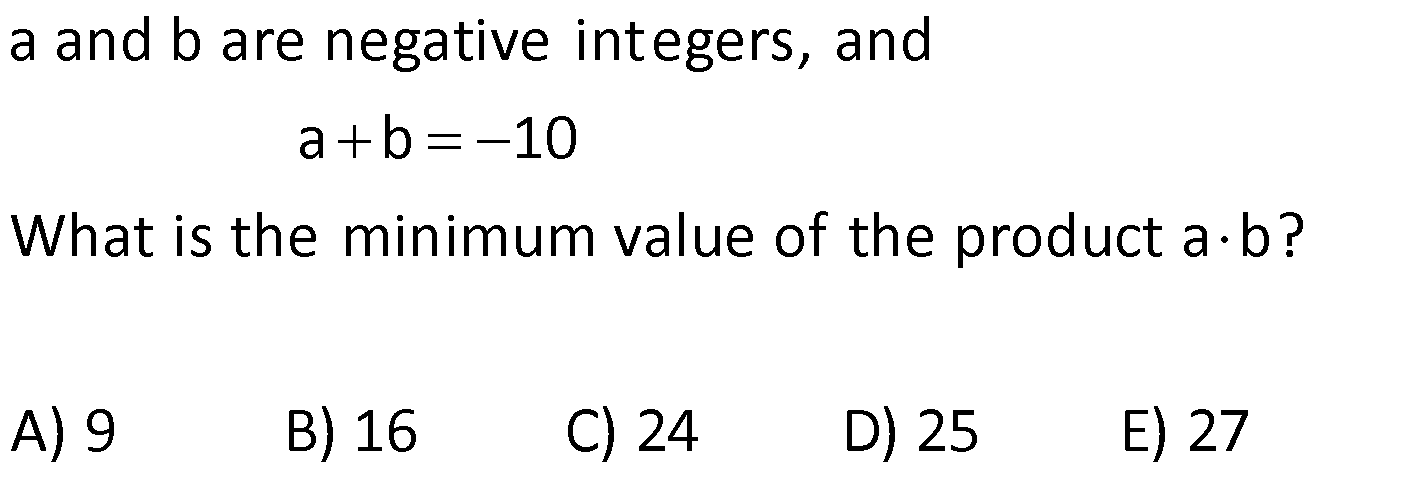

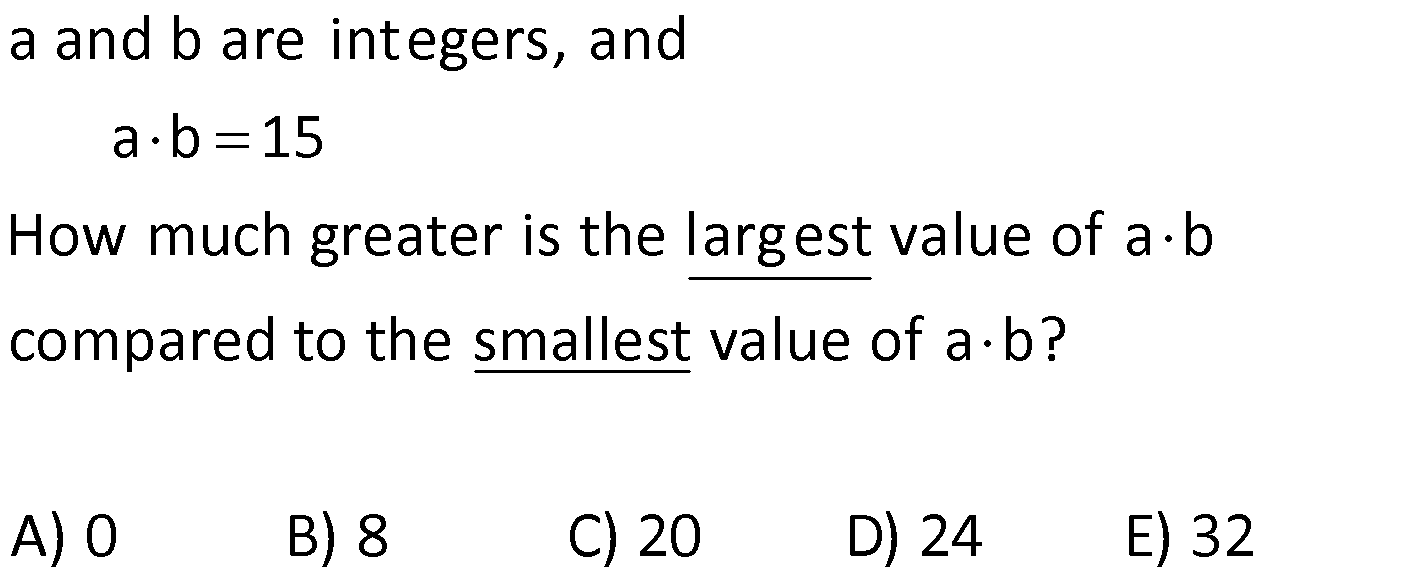



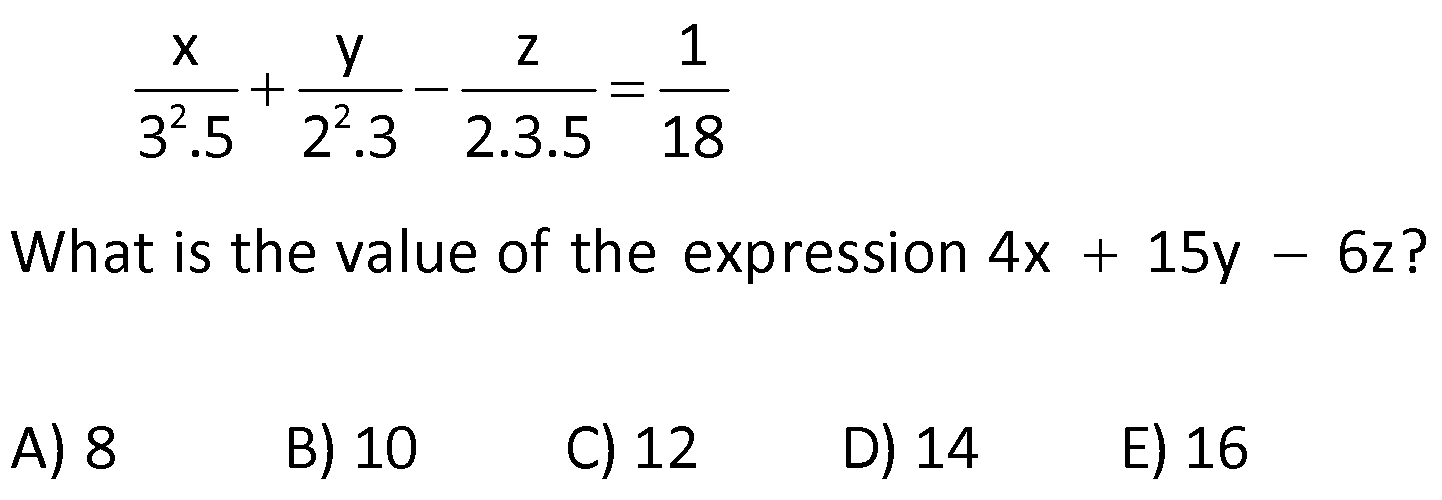

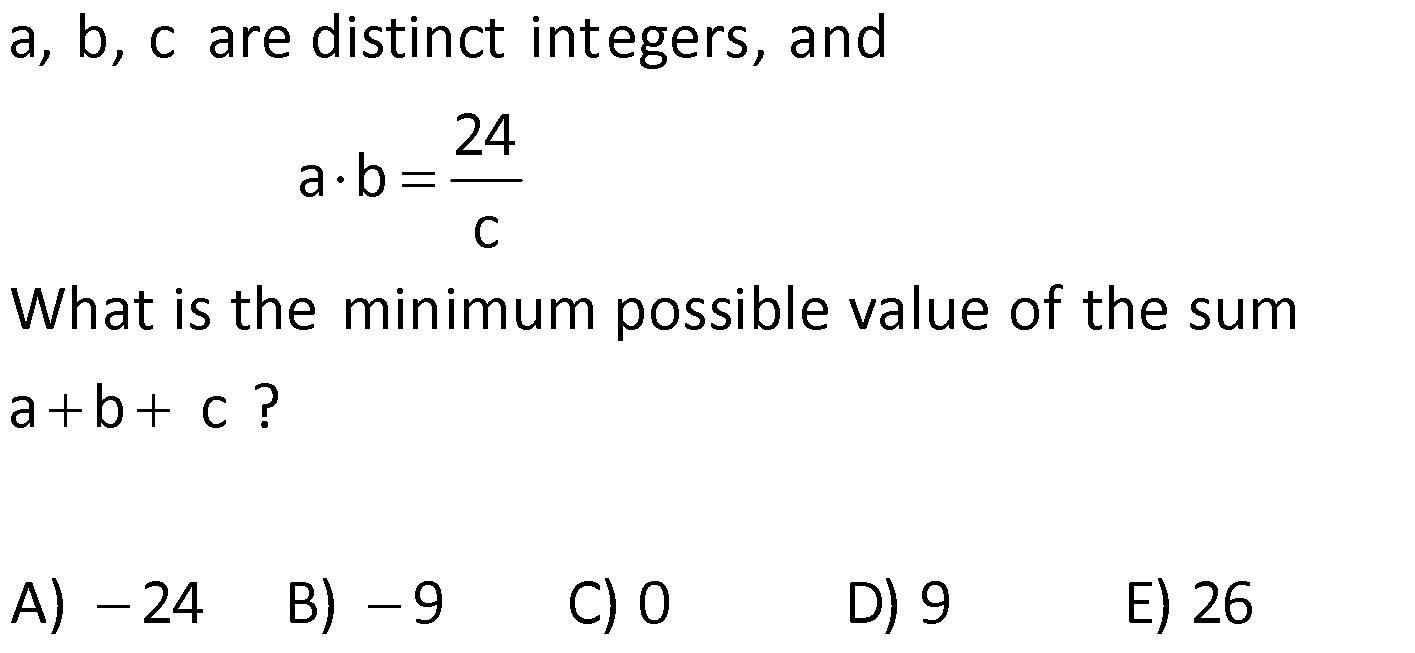
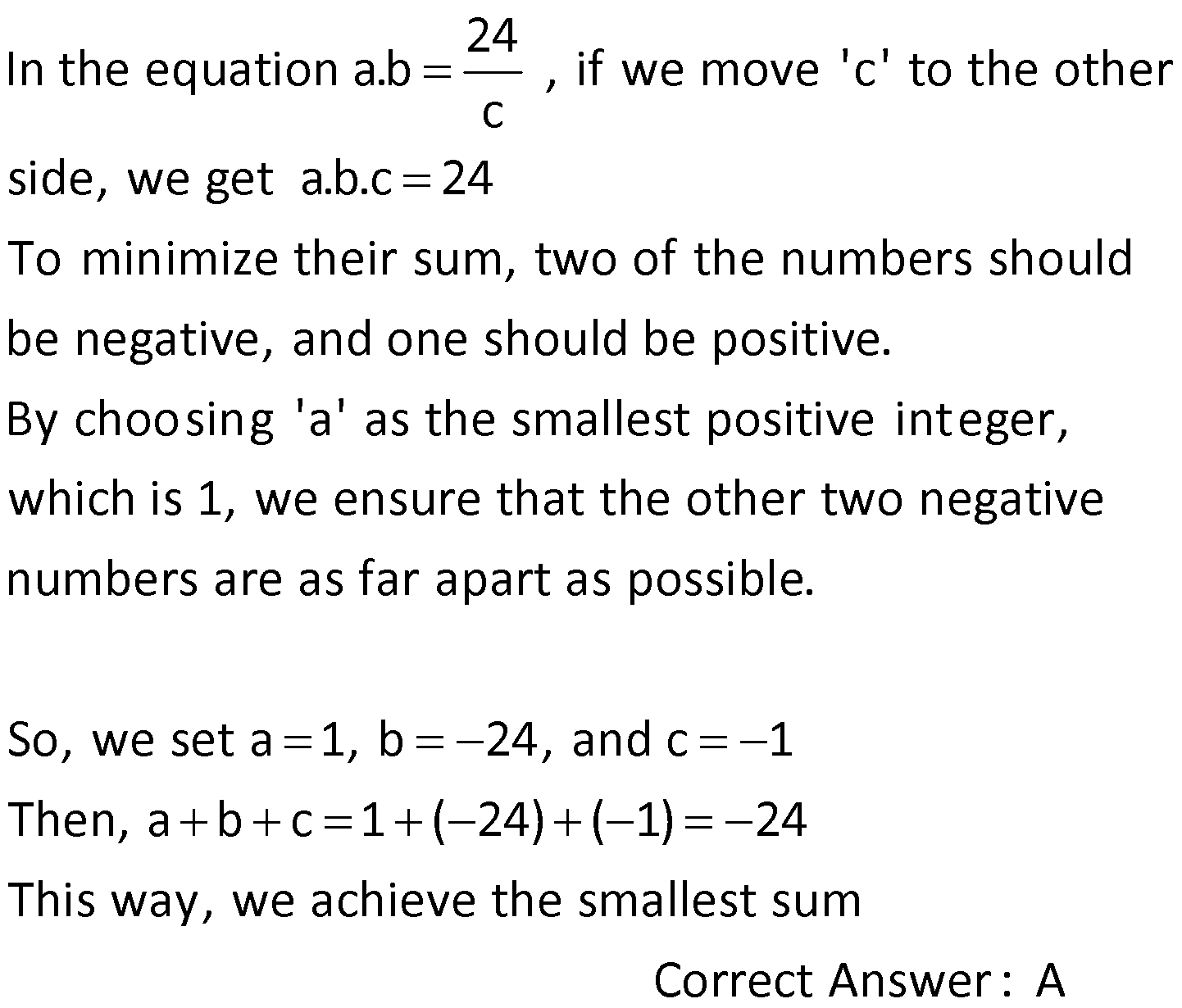
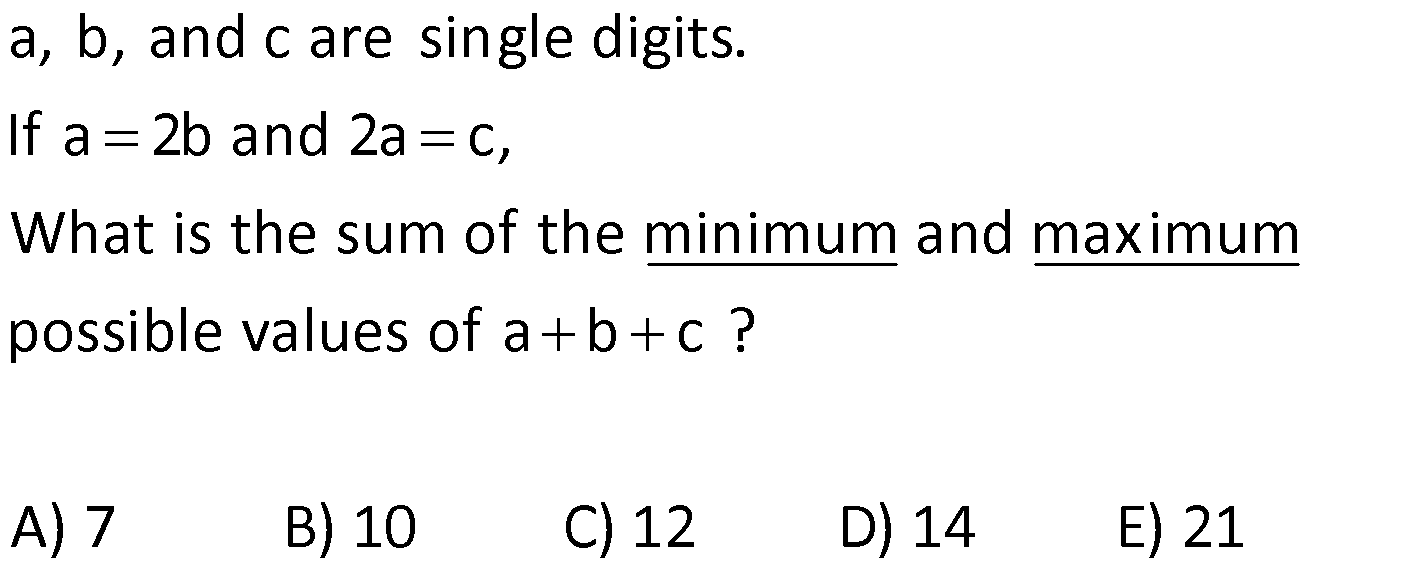

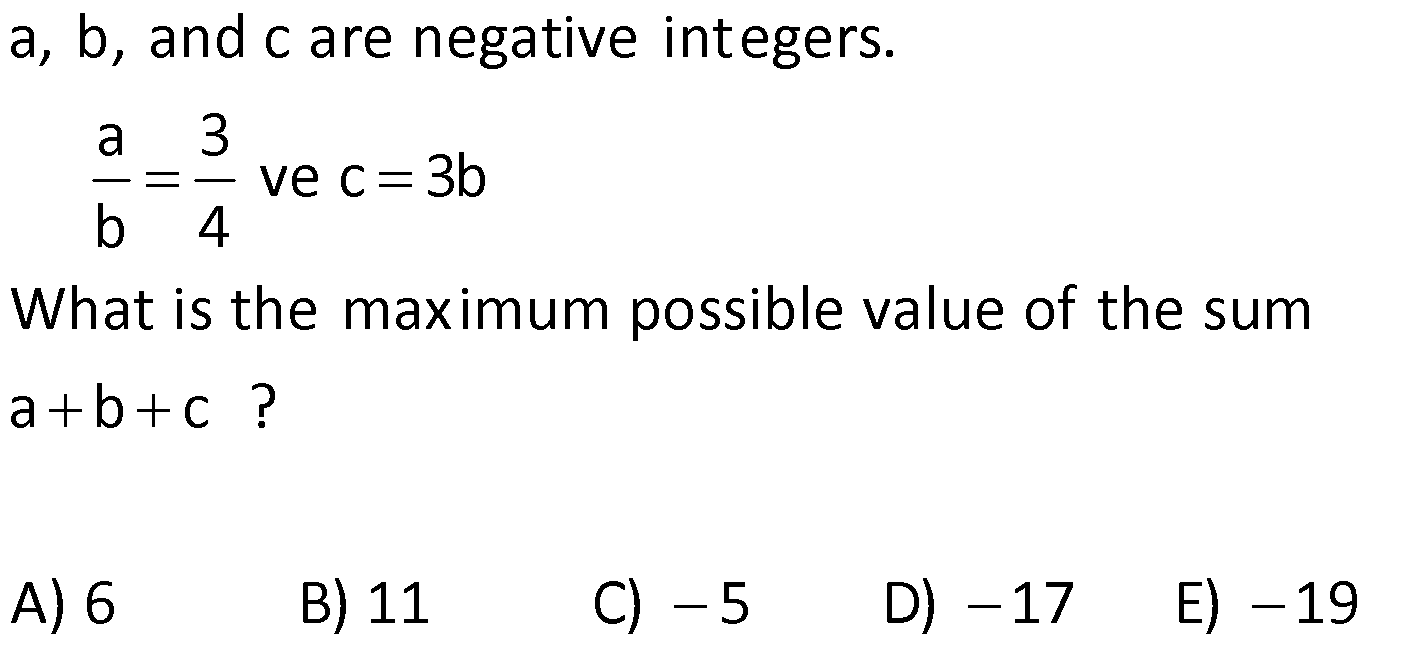

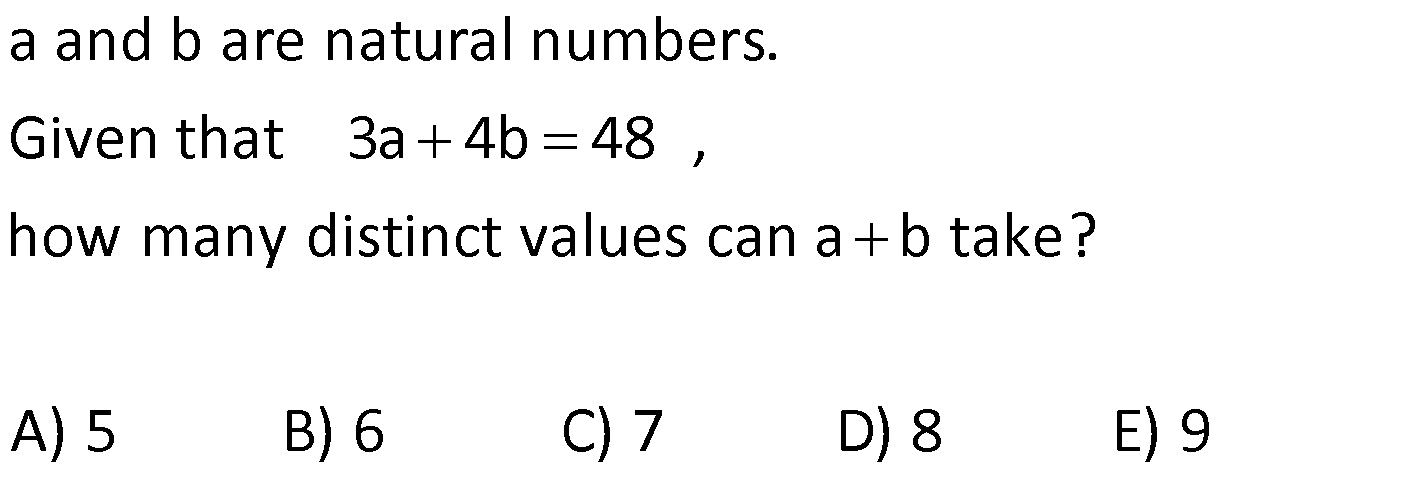





If you encounter any issues or wish to provide feedback regarding the questions or solutions, you can instantly convey them using the ‘Comment’ option located at the bottom of the page
BASIC CONCEPTS global.matematikkolay.net 1) positive integers, and then what is the sum of all possible values for b? A) 6 B) 10 C) 15 D) 18 E) 22 If a, b, c are distinct a 1 c , a b 12 b Solution: (b) Positive integers start at 1 and continue as 1, 2, 3, and so on. If we make some adjustments to the first equation provided in the question, we find the fo g a a 1 a w b 1 c c c a b bc b b llo ing It 1 is b r iven in the question that a b is equal to 12. Let’s substitute this value into the expression we found Let’s find the values of b and c b a b bc bc 12 b y substituting num e For b 1, c 12 , a 11 Fo rs. a, b, and c must be dist 1 inct , b 2, c 6 , a 0 For b 3 c 4 , f ro r m a 9 For b 4, c 3 , a 8 Fo b 6, c 2 , a 6 F or b 12, c 1 , a 0 each other. We cannot use them. a We cannot use them. The sum of the values taken by b is 1 2 3 4 10 is not a positive integer. Correct Answer : B 2) Given that a, b, and c are positive integers and What is the smallest possible value of a b c? A) 9 B) 10 C) 11 D) 12 E) 13 a b 5 a c 15 Solution: c In these types of questions, the variable that appears in multiple products should be assigned the largest possible value. Therefore, the variable “a” sho If a.b 5 t ul hen b o 1 I t f e a . c d b se t 5. 15 then Correct Answer : A 3 We obtained a b c 5 1 3 9 3) a, b, and c are positive integers and What is the largest possible value of a b c? A) 11 B) 21 C) 29 D) 32 E) 33 a b 12 a c 16 Solution: In this question,similar to the one above, the largest total value is sought. To achieve the maximum total value, the common factor should be as small as possible. Therefore, the variable “b” is assigned the smallest positive integer, which is 1. If is obtained If then c 16 is obtained. a b c 12 1 16 results in 29. Corre a.b 12, then a 12 . b.c 16, ct Answer : C 4) a, b, and c are integers and What is the smallest possible value of a b c? A) 10 B) 11 C) 20 D) 24 E) 29 a b 12 a c 16 BASIC CONCEPTS global.matematikkolay.net Solution: In this case, since the numbers are integers, you have the option to use negative integers as well. To minimize the total value of the numbers, it’s best to use negative integers. When working with negative integers, you should think in the opposite way compared to operations with positive integers. To achieve the smallest total value, the common factor should be the largest negative integer. So, in th If a.b 12, then a 12 If b.c 16, then c 16 a b c ( 12) ( 1) ( 16) 29 is case, the variable “b” is set to the largest negative integer, which is 1 (not 4). is the result. Correct Answer : E 5) Given that a and b are distinct positive integers, and What is the sum of the minimum and maximum possible values for the expression a b? A) 35 B) 40 C) 42 D) 46 E) 47 ab 12 Solution: In situations where the sum is given and you want to maximize the product, the numbers should be chosen close to each other. Conversely, when you want to minimize the product, the numbers should be selected far from each other. 5 In the question, a b 12 is given annot choose the same numbers since they w need t e b o be b dis c ti u n t c e t Th clos s n m ers a 6, 6 ( e ) The closest numbers a 7, b a.b 35 (The largest value) The closest numbers a 1, b 11 a.b 11 (The smal The sum of 35 and 11 is 46. l )e Corre e ct A s ns l we v r t u : D a 6) a and b are negative integers, and What is the minimum value of the product a b? A) 9 B) 16 C) 24 D) 25 E) 27 ab 10 Solution: To minimize their product, the numbers need to be chosen far apart from each other. In the given equation , the farthest numbers are a 1 and b 9 The product a.b equals 9, which is the smallest p a b 10 ossible value. Correct Answer : A 7) a and b are integers, and How much greater is the largest value of a b compared to the smallest value of a b? A) 0 B) 8 C) 20 D) 24 E) 32 a b 15 BASIC CONCEPTS global.matematikkolay.net Solution: To obtain the largest value of a b a and b should be positive, and they should be far apart from each other. In this case, if a 15 and b 1, then a b 16 To obtain the smallest value of a b a and b shoul d be negative, and they should be far apart from each other. In this case, if a 15 and b 1, then a b 16 The difference is 16 ( 16) 32 Correc t Answer : E 8) a and b are natural numbers, and What is the smallest value of the expression 5a 2b ? A) 16 B) 13 C) 11 D) 0 E) 12 ab 8 Solution: To find the smallest value of the expression 5a 2b, b should be the largest, and a should be the smallest. For the equation a.b 8, the smallest a is 1, and the largest b is 8. Therefore, the smallest v alue of 5a 2b is 5.1 2.8 5 16 11 Correct Answer : C 9) 2 2 What is the value of the expression 4x 15y 6z? A) 8 B) 10 C) 12 D) 14 E) 16 x y z 1 3 .5 2 .3 2.3.5 18 Solution: 2 2 2 2 2 2 2 (2 ) (3.5) (2.3) Let’s equalize the denominators in the expression To make all the denominators o x y z 1 have the same factors, we can expand them as foll ws : 3 .5 2 .3 2.3.5 18 x y z 1 4x 3 .5 2 .3 2.3.5 18 2 .3 .5 2 2 2 2 2 2 15y 6z 2 .3 .5 2 .3 .5 4x 15y 6z 1 2 .3 .5 18 4x 15y 6z 180 1 180 4x 15y 6z 18 18 4x 15y 6z 10 is obtaine B d. Correct Answer : 10) ntegers, and What is the minimum possible value of the sum a b c ? A) 24 B) 9 C) 0 D) 9 E) 26 a, b, c are distinct i 24 a b c Solution: In the equation if we move ‘c’ to the other side, we get a.b.c 24 To minimize their sum, two of the numbers should be negative, and one should be positive. By choosing ‘a’ as the smallest pos 24 a.b , c itive integer, which is 1, we ensure that the other two negative numbers are as far apart as possible 1 ( 24 . ) ( So, we set a 1, b 24, and c 1 Then, a b c This way, we achieve the smalle s 1) 24 st um Correct Answer : A BASIC CONCEPTS global.matematikkolay.net 11) a, b, and c are single digits. If a 2b and 2a c, What is the sum of the minimum and maximum possible values of a b c ? A) 7 B) 10 C) 12 D) 14 E) 21 Solution: The digits are 0, 1, 2, 3, …, 9. The question states that a 2b and 2a c By substituting 2b for a in the equation 2a c, we obtain the equation 4b c The values of a, b, and c are then 2b, b, and 4b, resp ectively. To find the largest values, we should assign the highest possible value to b. However, the expression 4b should not exceed the highest digit, which is 9. Therefore, b can be at most 2. The largest values for which results in a b c 14 For the smallest value, we can choose b to be 0. Since the question did not specify that the digits should be distinct, there is no issue a, b, c 2b, b, 4b 4, 2, 8 with the digits being the same. The values for a, b, and c are then 2b, b, and 4b 0, 0, 0, which results in a b c 0 So, the total is 14 0 14. Corre ct Answer : D 12) a, b, and c are negative integers. hat is the maximum possible value of the sum a b c ? A) 6 B) 11 C) 5 D) 17 E) 19 a 3 ve c 3b b 4 W Solution: First, it’s helpful to express the equation c 3b in fractional form. We now have two fractional equations. In such questions, it’s convenient to make the common factor of the coeffi c 3 c 3b b 1 -4 cients the same to reach a solution more easily. By making the coefficients of the common factor the same, we can express a, b, and c as multiples of a common f a 3 c 3 a 3 c 12 ve ve b 4 b 1 b 4 b 4 actor, let’s call it “k.” This results in a 3k, b 4k, and c 12k. Since a, b, and c are stated to be negative, we choose k to be 1 to maximize their va lues. As a result, a 3, b 4, and c 12 Correct Answer : E ab c (3) (4) (12) 19 13) a and b are natural numbers. how many distinct values can a b take? A) 5 B) 6 C) 7 D) 8 E) 9 Given that 3a 4b 48 , Solution: In the expression 3a 4b 48, the possible values for a are multiples of the number in front of b, while the values for b are multiples of the number in front of a. When a increases by 4 units, b decreases by 3 units. When a 0, b 12, a b 12 When a 4, b 9, a b 13 When a 8, b 6, a b 14 When a 12, b 3, a b 15 When a 16, b 0, a b 16 BASIC CONCEPTS global.matematikkolay.net So, a b takes 5 different values. Correct Answer : A 14) a, b, and c are distinct natural numbers. What is the largest possible value that c can take? A) 19 B) 20 C) 21 D) 22 E) 23 5a 4b 3c 75 Solution: In the expression 5a 4b 3c 75, to find the largest possible value for c, we start by assigning the lowest possible values to the coefficients other than c. We can use the smallest natural number, which i s 0, for a. Since the question states that the numbers are distinct, we assign the next smallest natur 5a 4b 3c 75 a 0 1 l number, 1, to b x c does not come out as an intege . 0 r c does not come out as an integer. The value of c is found to be 21 Correct Answer : C 2 x 0 3 21 15) Let x and y be two digit natural numbers, and x y 36 How many different values of x satisfy this equation? A) 53 B) 54 C) 55 D) 56 E) 57 Solution: In the expression x y 36, to find how many different values x can take, we need to determine the largest and smallest values for x. x can be as large as the largest two digit natural number, which is 99 F i x 10 36 o x r the smallest value of x, we assign the smallest two digit natural number, which is 10, to y is the smallest value. This means that x can take all values from 46 to 99. No. of consecut 46 99 46 1 54 Correct Answer : B ve terms Last Term First Term 1 The number of values for x